Comunicaciones de las VII Jornades de la SEMCV Alacant06
1. Francesc Pastor Verdú. La Pissarra Digital Interactiva: una eina per a la construcció de coneixements matemàtics en educació infantil i primària
La present comunicació descriu les possibilitats didàctiques de la Pissarra Digital Interactiva a l’Educació Infantil i Primària, i més concretament a l’àrea curricular de les Matemàtiques. Sobre la base fonamental de constituir una “finestra màgica” amb la integració al seu si dels diversos elements multimèdia (imatge fixa, vídeo, so, text) i la nova fórmula d’interacció amb ella (tàctil), es garanteix un gran potencial motivacional i atencional. Però, a més a més, també és destaca la conveniència del seu aprofitament per a la construcció de coneixements matemàtics des d’enfocaments investigatius i participatius en grup, aspecte este al qual contribueix la PDI si la considerem un instrument generador d’interaccions i aprenentatge social.
MAURICIO CONTRERAS DEL RINCÓN
I.E.S. BENICALAP. VALENCIA
Hace ya muchos años que Leonardo de Pisa, alias Fibonacci, planteó (y resolvió) su célebre problema sobre la reproducción de los conejos. Fue concretamente en 1202 cuando apareció su famoso “libro del ábaco”, donde publicó sus trabajos, dando luz a la conocida sucesión: 1, 1, 2, 3, 5, 8, 13, ...
En otra época totalmente diferente, Blaise Pascal (1623−1662) publicó un curioso triángulo numérico que utilizó para resolver problemas de recuentos y cálculo de probabilidades. También Nicolo Fontana, apodado Tartaglia (1500−1557) utilizaba el mismo triángulo para sus trabajos...
Pero ninguno de los tres sospechaba (ni por asomo) que a mediados del siglo XX volverían a ponerse de actualidad sus trabajos gracias a unos nuevos y sorprendentes objetos matemáticos denominados fractales. A partir de su descubrimiento por Benoît Mandelbrot en 1975, los fractales empezaron a aparecer hasta en la sopa y nuevas palabras como “atractor”, “caos”, “auto−organización” hicieron su aparición en algunos textos destinados a la enseñanza.
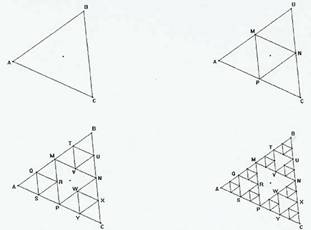
Partiendo del antecedente en USA de Peitgen, Jürgens, Saupe (FRACTALS FOR THE CLASSROOM, 1991), hemos llevado los fractales al aula de... primer ciclo de la E.S.O. y los estudiantes han observado las conexiones entre la sucesión de Fibonacci, el triángulo de Pascal, la divisibilidad, el fractal de Sierpinski y la teoría del caos. En esta comunicación mostramos los trabajos y conclusiones de los estudiantes.

3. Joan Pons. El concurs de resolució de problemes Enginy
Joan Pons. IES Mutxamel. Mutxamel
GRUP DE TREBALL ENGINY
Concurs comarcal de matemàtiques
Objectiu general de treball.
Divulgació de les matemàtiques a través de la resolució de problemas.
Afavorir una actitud positiva cap a les matemàticas entre l’alumnat.
Estimular com a positiu l’activitat matemàtica fora de l’aula.
Resoldre problemes utilitzant diferents estratègies.
Coordinació amb diferents centres de la comarca de l’Alacantí.
Nivell educatiu.
Dirigit, especialment, a l’alumnat d’Ensenyament Secundari (ESO, Batxillerat, i Mòduls professionals). Però degut al seu carácter obert podran participar, també, totes les persones de la comarca.
Tema específic.
Treball extraescolar plantejat com un concurs comarcal de resolució de problemes.
Els departaments de matemàtiques que participen són:
IES Berlanga, de Sant Joan
IES Clot de l’Illot, de El Campello.
IES Enric Valor, de El Campello.
IES Loixa, de Sant Joan.
IES Mutxamel
Secció de l’IES Mutxamel
IES Xixona
Index.
Bases.
Problemes.
Estadística de la participació.
Llistat de persones que hi participen.
Model de respostes de l’alumnat
Desenvolupament de la comunicació.
1. Competicions matemàtiques clàssiques: Olimpíades, Cangur, ...
2. Competicions matemàtiques no presencials: Open’s, Proves a l’esprint, ...
3. Internet i e-mail: Recursos per a facilitar l’organització.
4. Estructura i experiència del grup de treball ENGINY.
5. Conclusions.
4. Joan Pons i Fernando Arenas. Una aproximació al raonament emprat per l’alumnat en la resolució del problemes
Joan Pons. IES Mutxamel
Fernando Arenas. Ext. IES Mutxamel
5. María Sala. Mosaicos de Escher, y más, en un proyecto de centro.
María Sala. IES Las Lomas. Alicante
6. Federico Riquelme y Daniel Climent. Trabajo con alumnos de alto rendimiento. Proyecto esfera terrestre
Federico Riquelme y Daniel Climent. IES Badia de Baver. Alacant
Dentro del proyecto de trabajo con alumnos de alto rendimiento, surge esta programación conjunta en las asignaturas de Ciencias de la Naturaleza y Matemáticas sobre la esfera terrestre, sus movimientos y consecuencias.
- Los contenidos de Ciencias a desarrollar son la Tierra y el clima.
- Los contenidos de Matemáticas en ese bloque son semejanza y trigonometría.
El método de trabajo está basado en la realización de experiencias diversas e investigaciones que sirvan a los alumnos como elemento de motivación y motor de búsqueda.
Utilizamos varios centros de interés de gran repercusión en los medios de comunicación para desarrollar los tres bloques fundamentales:
- Equinoccio de otoño (determinación del equinoccio de otoño, del mediodía solar y de la inclinación de los rayos solares a partir de la sombra producida por un gnomon)
- Huracán Katrina (huracanes otoñales en el Caribe)
- Eclipse anular de sol (establecimiento de las distancias y relaciones volumétricas entre Luna, Tierra y Sol a partir de los eclipses)
7. Alfred Monxo. Matemáticas y convivencia. Primaria.
8. Daniel Vila. El cálculo en bachillerato y la nueva calculadora gráfica 9860 G SD.
9. Pedro A. Pomata, y otros. Un modelo matemático para la propagación del conocimiento científico
Pedro Antonio Pomata Varó
IES Virgen del Remedio de Alicante. E–mail: pa.pomata@telefonica.net
Fernando Miguel Pérez Herranz
Universidad de Alicante. E–mail: Perez.Herranz@ua.es
José Ignacio Úbeda García
Universidad de Alicante. E–mail: jiug@ua.es
José Manuel Iñesta Quereda
Universidad de Alicante. E–mail: inesta@dlsi.ua.es
En esta comunicación se exponen el trabajo que propone un modelo fractal para dar cuenta del fenómeno de propagación de la ciencia, lo que nos permite sacar algunas consecuencias sobre un capítulo de la epistemología de gran repercusión a partir de los trabajos de Kuhn: la transmisión, aceptación y estabilización del conocimiento científico.
10. Antonio Giner. LA COMUNICACIÓN DOCENTE EN EL AULA: tres breves consideraciones.
Antonio Giner Gomis
Universitat d'Alacant. E–mail: a.giner@ua.es
Quizás la comunicación que establecemos en el aula sea una práctica tan familiar como rutinaria que sobre ella no lleguemos a centrar nuestra atención; y que, por tanto, pueda observarse como un elemento didáctico desprovisto de interés. Pero lo familiar, como decía el psiquiatra cordobés Castilla del Pino, no por ello es conocido. La comunicación en el aula resulta ser, como afirma De la Torre (2000) el corazón de la didáctica, aunque también ha de aclararse que la enseñanza no se puede reducir a sólo comunicación; las relaciones de comunicación en el aula, movilizan, dan vida, insuflan energía a los demás elementos didácticos (objetivos, contenidos, organización, evaluación, etc.), o, tal vez, los reconvierta en sombríos elementos encaminados a conseguir el éxito de aquel proyecto educativo rotulado la negación del ser.
Propongo revisitar el ámbito comunicativo del docente en el aula para observarlo desde tres perspectivas diferentes que nos puedan ofrecer algún tipo de fundamentación y razonamientos con los que mantener esa actitud de alerta y cuidado frente a uno de los componentes didácticos más valiosos para llevar a cabo de manera satisfactoria, gratificante y valiosa el acto educativo.
Para ello nuestra propuesta considerará tres miradas sobre la comunicación en el aula:
a. la comunicación como aprendizaje y práctica que requiere esfuerzo y sentido.
b. La comunicación y su relación indesligable con el comunicante
c. La comunicación como tarea de actualización en la formación docente
11. David Arnau. El nombre en els diferents currículums d’Educació Infantil i la Didàctica de la Matemàtica: dos camins divergents.
David Arnau Vera
Universitat de València. E–mail: david.arnau@uv.es
¿S’ha d’ensenyar a comptar als alumnes d’Educació Infantil? ¿I en cas afirmatiu s’ha de reduir a la memorització d’una cançoneta o hem de possibilitar que els alumnes elaboren la seqüència numèrica fins a convertir-la en un instrument per a fer matemàtiques? Freudenthal (1973, p. 171) ja va indicar que “El nombre per a comptar es converteix en l’objecte irreemplaçable per a l’activitat de calcular... La seqüència numèrica és la base sobre la que s’han de construir les matemàtiques... Sense la seqüència numèrica no hi ha matemàtiques”. Tanmateix, la manca d’instruccions clares i detallades dins de les especificacions curriculars no permeten saber quines són les competències que han d’assolir els alumnes d’Educació Infantil. A més a més, l’oposició que mostren alguns mestres al canvi, la interpretació extrema de principis pedagògics com la no memorització o que l’alumne ha de construir el coneixement..., així com les idees piagetianes de què els alumnes d’Educació Infantil no poden accedir al nombre, han produït que l’ensenyament de la seqüència numèrica es faça de manera poc sistemàtica. En aquesta comunicació presentarem observacions teòriques i pràctiques que desenvolupen les idees anteriors.